Entries for tag "algorithms", ordered from most recent. Entry count: 68.
# DivideRoundingUp Function and the Value of Abstraction
Sun
25
Sep 2022
It will be a brief article. Imagine we implement a postprocessing effect that needs to recalculate all the pixels on the screen, reading one input texture as SRV 0 and writing one output texture as UAV 0. We use a compute shader that has numthreads(8, 8, 1) declared, so each thread group processes 8 x 8 pixels. When looking at various codebases in gamedev, I've seen many times a code similar to this one:
renderer->SetConstantBuffer(0, &computeConstants);
renderer->BindTexture(0, &inputTexture);
renderer->BindUAV(0, &outputTexture);
constexpr uint32_t groupSize = 8;
renderer->Dispatch(
(screenWidth + groupSize - 1) / groupSize,
(screenHeight + groupSize - 1) / groupSize,
1);
It should work fine. We definitely need to align up the number of groups to dispatch, so we don't skip pixels on the right and the bottom edge in case our screen resolution is not a multiply of 8. The reason I don't like this code is that it uses a "trick" that in my opinion should be encapsulated like this:
uint32_t DivideRoundingUp(uint32_t a, uint32_t b)
{
return (a + b - 1) / b;
}
...
renderer->Dispatch(
DivideRoundingUp(screenWidth, groupSize),
DivideRoundingUp(screenHeight, groupSize),
1);
Abstraction is the fundamental concept of software engineering. It is hard to work with complex systems without hiding details behind some higher-level abstraction. This idea applies to entire software modules, but also to small, 1-line pieces of code like this one above. For some programmers it might be obvious when seeing (a + b - 1) / b that we do a division with rounding up, but a junior programmer who just joined the team may not know this trick. By moving it out of view and giving it a descriptive name, we make the code cleaner and easier to understand for everyone. Therefore I think that all small arithmetic or bit tricks like this should be enclosed in a library of functions rather than used inline. Same with the popular formula for checking if a number is a power of two:
bool IsPow2(uint32_t x)
{
return (x & (x - 1)) == 0;
}
Comments | #software engineering #algorithms #c++ Share
# A Metric for Memory Fragmentation
Wed
06
Apr 2022
In this article, I would like to discuss the problem of memory fragmentation and propose a formula for calculating a metric telling how badly the memory is fragmented.
The problem can be stated like this:
So it is a standard memory allocation situation. Now, I will explain what do I mean by fragmentation. Fragmentation, for this article, is an unwanted situation where free memory is spread across many small regions in between allocations, as opposed to a single large one. We want to measure it and preferably avoid it because:
VirtualAlloc) and sub-allocating them for the user's allocation requests, high fragmentation my require allocating another block to satisfy the request, making the program using more system memory than really needed.A solution to this problem is to perform defragmentation - an operation that moves the allocations to arrange them next to each other. This may require user involvement, as pointers to the allocations will change then. It may also be a time-consuming operation to calculate better places for the allocations and then to copy all their data. It is thus desirable to measure the fragmentation to decide when to perform the defragmentation operation.
Comments | #gpu #algorithms #optimization Share
# Intrusive Linked List in C++
Tue
25
May 2021
A doubly linked list is one of the most fundamental data structures. Each element contains, besides the value we want to store in this container, also a pointer to the previous and next element. This may not be the best choice for indexing i-th element or even traversing all elements quickly (as they are scattered in memory, performance may suffer because of poor cache utilization), but inserting an removing an element from any place in the list is quick.
![]()
Source: Doubly linked list at Wikipedia.
Inserting and removing elements is quick, but not necessarily very simple in terms of code complexity. We have to change pointers in the current element, previous and next one, as well as handle special cases when the current element is the first one (head/front) or the last one (tail/back) – a lot of special cases, which may be error-prone.
Therefore it is worth to encapsulate the logic inside some generic, container class. This authors of STL library did by defining List class inside #include <list>. It is a template, where each item of the list will contain our type T plus additional data needed – most likely pointer to the next and previous item.
struct MyStructure {
int MyNumber;
};
std::list<MyStructure> list;
list.push_back(MyStructure{3});
In other words, our structure is contained inside one that is defined internally by STL. After resolving template, it may look somewhat like this:
struct STL_ListItem {
STL_ListItem *Prev, *Next;
MyStructure UserData;
};
What if we want to do the opposite – to contain “utility” pointers needed to implement the list inside our custom structure? Maybe we have a structure already defined and cannot change it or maybe we want each item to be a member of two different lists, e.g. sorted by different criteria, and so to contain two pairs of previous-next pointers? A definition of such structure is easy to imagine, but can we still implement some generic class of a list to hide all the complex logic of inserting and removing elements, which would work on our own structure?
struct MyStructure {
int MyNumber = 0;
MyStructure *Prev = nullptr, *Next = nullptr;
};
If we could do that, such data structure could be called an “intrusive linked list”, just like an “intrusive smart pointer” is a smart pointer which keeps reference counter inside the pointed object. Actually, all that our IntrusiveLinkedList class needs to work with our custom item structure, besides the type itself, is a way to access the pointer to the previous and next element. I came up with an idea to provide this access using a technique called “type traits” – a separate structure that exposes specific interface to deliver information on some other type. In our case, it is to read (for const pointer) or access by reference (for non-const pointer) the previous and next pointer.
The traits structure for MyStructure may look like this:
struct MyStructureTypeTraits {
typedef MyStructure ItemType;
static ItemType* GetPrev(const ItemType* item) { return item->Prev; }
static ItemType* GetNext(const ItemType* item) { return item->Next; }
static ItemType*& AccessPrev(ItemType* item) { return item->Prev; }
static ItemType*& AccessNext(ItemType* item) { return item->Next; }
};
By having this, we can implement a class IntrusiveLinkedList<ItemTypeTraits> that will hold a pointer to the first and last item on the list and be able to insert, remove, and do other operations on the list, using a custom structure of an item, with custom pointers to previous and next item inside.
IntrusiveLinkedList<MyStructureTypeTraits> list;
list.PushBack(new MyStructure{1});
list.PushBack(new MyStructure{2});
for(MyStructure* i = list.Front(); i; i = list.GetNext(i))
printf("%d\n", i->MyNumber); // prints 1, 2
while(!list.IsEmpty())
delete list.PopBack();
I know this is nothing special, there are probably many such implementations on the Internet already, but I am happy with the result as it fulfilled my specific need elegantly.
To see the full implementation of my IntrusiveLinkedList class, go to D3D12MemAlloc.cpp file in D3D12 Memory Allocator library. One caveat is that the class doesn't allocate or free memory for the list items – this must be done by the user.
Comments | #algorithms #c++ Share
# Operations on power of two numbers
Sun
09
Sep 2018
Numbers that are powers of two (i.e. 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 and so on...) are especially important in programming, due to the way computers work - they operate on binary representation. Sometimes there is a need to ensure that certain number is power of two. For example, it might be important for size and alignment of some memory blocks. This property simplifies operations on such quantities - they can be manipulated using bitwise operations instead of arithmetic ones.
In this post I'd like to present efficient algorithms for 3 common operations on power-of-2 numbers, in C++. I do it just to gather them in one place, because they can be easily found in many other places all around the Internet. These operations can be implemented using other algorithms as well. Most obvious implementation would involve a loop over bits, but that would give O(n) time complexity relative to the number of bits in operand type. Following algorithms use clever bit tricks to be more efficient. They have constant or logarithmic time and they don't use any flow control.
1. Check if a number is a power of two. Examples:
IsPow2(0) == true (!!) IsPow2(1) == true IsPow2(2) == true IsPow2(3) == false IsPow2(4) == true IsPow2(123) == false IsPow2(128) == true IsPow2(129) == false
This one I know off the top of my head. The trick here is based on an observation that a number is power of two when its binary representation has exactly one bit set, e.g. 128 = 0b10000000. If you decrement it, all less significant bits become set: 127 = 0b1111111. Bitwise AND checks if these two numbers have no bits set in common.
template <typename T> bool IsPow2(T x)
{
return (x & (x-1)) == 0;
}
2. Find smallest power of two greater or equal to given number. Examples:
NextPow2(0) == 0 NextPow2(1) == 1 NextPow2(2) == 2 NextPow2(3) == 4 NextPow2(4) == 4 NextPow2(123) == 128 NextPow2(128) == 128 NextPow2(129) == 256
This one I had in my library for a long time.
uint32_t NextPow2(uint32_t v)
{
v--;
v |= v >> 1; v |= v >> 2; v |= v >> 4; v |= v >> 8;
v |= v >> 16;
v++;
return v;
}
uint64_t NextPow2(uint64_t v)
{
v--;
v |= v >> 1; v |= v >> 2; v |= v >> 4; v |= v >> 8;
v |= v >> 16; v |= v >> 32;
v++;
return v;
}
3. Find largest power of two less or equal to given number. Examples:
PrevPow2(0) == 0 PrevPow2(1) == 1 PrevPow2(2) == 2 PrevPow2(3) == 2 PrevPow2(4) == 4 PrevPow2(123) == 64 PrevPow2(128) == 128 PrevPow2(129) == 128
I needed this one just recently and it took me a while to find it on Google. Finally, I found it in this post on StackOveflow.
uint32_t PrevPow2(uint32_t v)
{
v |= v >> 1; v |= v >> 2; v |= v >> 4; v |= v >> 8;
v |= v >> 16;
v = v ^ (v >> 1);
return v;
}
uint64_t PrevPow2(uint64_t v)
{
v |= v >> 1; v |= v >> 2; v |= v >> 4; v |= v >> 8;
v |= v >> 16; v |= v >> 32;
v = v ^ (v >> 1);
return v;
}
Update 2018-09-10: As I've been notified on Twitter, C++20 is also getting such functions as standard header <bit>.
Comments | #math #c++ #algorithms Share
# How to check if an integer number is a power of 10?
Wed
04
Oct 2017
I was recently asked a test question to write a function that would check whether a given integer number is a power of ten. I didn't know the answer immediately because I never solved this puzzle before, so I needed to think about a solution. I quickly came to a conclusion that there are many possible solutions, so I later decided to write them down and share with you.
Number is a power of 10 if it's equal to 10, 100, 1000 etc. 1 is also 0-th power of 10. Other numbers like 2, 3, 11, 12 etc. are not powers of 10. 0 and all negative numbers should also be rejected.
Below you can find 5 different solutions - all of them correct, but some of them more efficient than others. Example code is in C, but you can easily implement the same algorithms in Java or any other programming language.
First thing that came to my mind was to convert the number to a string and check whether it contains '1' followed by '0'-s.
int IsLog10_v1(int32_t x)
{
// Convert x to string.
char buf[12];
itoa(x, buf, 10);
const size_t bufLen = strlen(buf);
// Check if string contains '1' followed by '0'-s.
if(buf[0] != '1')
return 0;
for(size_t i = 1; i < bufLen; ++i)
{
if(buf[i] != '0')
return 0;
}
return 1;
}
Another option is to convert the number to floating-point format, use "real" log10 function, and check if the result is an integer. Note that double must be used here, because float has too small precision and would incorrectly return 1 for inputs like: 999999999, 1000000001.
int IsLog10_v2(int32_t x)
{
// Convert x to double. Calculate log10 of it.
double x_d = (double)x;
double x_log10 = log10(x_d);
// Check if result is integer number - has zero fractional part.
return x_log10 - floor(x_log10) == 0.0;
}
If we want to operate on integer numbers only, we may come up with a recursive algorithm that checks whether the number is greater than zero, divisible by 10 and then calls the same function for x/10.
int IsLog10_v3(int32_t x)
{
if(x <= 0)
return 0;
if(x == 1)
return 1;
if(x % 10 != 0)
return 0;
// Recursion.
return IsLog10_v3(x / 10);
}
Because it's a tail recursion, it's easy to convert it to iterative algorithm (use loop instead of recursive call).
int IsLog10_v4(int32_t x)
{
if(x <= 0)
return 0;
// Same algorithm as v3, but converted from recursion to loop.
for(;;)
{
if(x == 1)
return 1;
if(x % 10 != 0)
return 0;
x /= 10;
}
}
Finally, the most efficient solution is to notice that there are only few possible powers of 10 in the range of 32-bit integers, so we can just enumerate them all.
int IsLog10_v5(int32_t x)
{
// Just enumerate all possible results.
return
x == 1 ||
x == 10 ||
x == 100 ||
x == 1000 ||
x == 10000 ||
x == 100000 ||
x == 1000000 ||
x == 10000000 ||
x == 100000000 ||
x == 1000000000;
}
You can find full source code as a simple, complete C program together with tests on my GitHub, as file: IsLog10.c.
Comments | #c #algorithms Share
# How to Flip Triangles in Triangle Mesh
Sat
19
Jan 2013
Given triangle mesh, as we use it in real-time rendering of 3D graphics, we say that each triangle have two sides, depending on whether its vertices are oriented clockwise or counterclockwise from particular point of view. In Direct3D, by default, triangles oriented clockwise are considered front-facing and they are visible, while triangles oriented counterclockwise are invisible because they are discarded by the API feature called backface culling.
When we have backface culling enabled and we convert mesh between coordinate systems, we sometimes need to "flip triangles". When vertices of each triangle are separate, an algorithm for this is easy. We just need to swap first with third vertex of each triangle (or any other two vertices). So we can start implementing the flipping method like this:

class CMesh
{
...
D3D11_PRIMITIVE_TOPOLOGY m_Topology;
bool m_HasIndices;
std::vector<SVertex> m_Vertices;
std::vector<uint32_t> m_Indices;
};
void CMesh::FlipTriangles()
{
if(m_Topology == D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST)
{
if(m_HasIndices)
FlipTriangleListInArray<uint32_t>(m_Indices);
else
FlipTriangleListInArray<SVertex>(m_Vertices);
}
...
}
Where the function template for flipping triangles in a vector is:
template<typename T>
void CMesh::FlipTriangleListInArray(std::vector<T>& values)
{
for(size_t i = 0, count = values.size(); i < count - 2; i += 3)
std::swap(values[i], values[i + 2]);
}
Simple reversing all elements in the vector with std::reverse would also do the job. But things get complicated when we consider triangle strip topology. (I assume here that you know how graphics API-s generate orientation of triangles in a triangle strip.) Reversing vertices works, but only when number of vertices in the strip is odd. When it's even, triangles stay oriented in the same way.
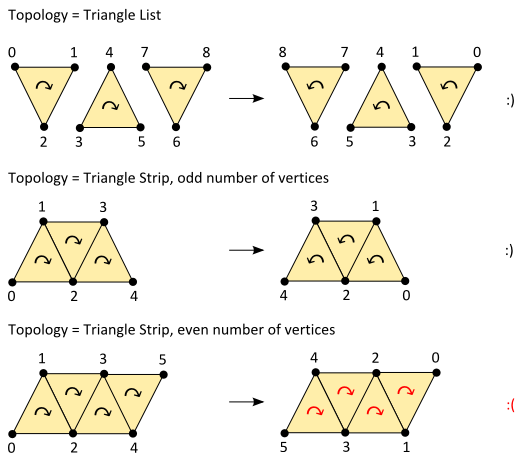
I asked question about this on forum.warsztat.gd (in Polish). User albiero proposed following solution: just duplicate first vertex. It will generate additional degenerate (invisible) triangle, but thanks to this all following triangles will be flipped. It seems to work!

I also wanted to handle strip-cut index (a special value -1 which starts new triangle strip), so the rest of my fully-featured algorithm for triangle flipping is:
...
else if(m_Topology == D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP)
{
if(m_HasIndices)
{
size_t begIndex = 0;
while(begIndex < m_Indices.size())
{
const size_t indexCount = m_Indices.size();
while(begIndex < indexCount && m_Indices[begIndex] == UINT_MAX)
++begIndex;
if(begIndex == indexCount)
break;
size_t endIndex = begIndex + 1;
while(endIndex < indexCount && m_Indices[endIndex] != UINT_MAX)
++endIndex;
// m_Indices.size() can change here!
FlipTriangleStripInArray<uint32_t>(m_Indices, begIndex, endIndex);
begIndex = endIndex + 1;
}
}
else
FlipTriangleStripInArray<SVertex>(m_Vertices, 0, m_Vertices.size());
}
}
Where function template for flipping triangles in selected part of a vector is:
template<typename T>
void CMesh::FlipTriangleStripInArray(std::vector<T>& values, size_t begIndex, size_t endIndex)
{
const size_t count = endIndex - begIndex;
if(count < 3) return;
// Number of elements (and triangles) is odd: Reverse elements.
if(count % 2)
std::reverse(values.begin() + begIndex, values.begin() + endIndex);
// Number of elements (and triangles) is even: Repeat first element.
else
values.insert(values.begin() + begIndex, values[begIndex]);
}
Comments | #directx #rendering #algorithms Share
# Iterating Backward using Unsigned Numbers
Thu
01
Mar 2012
I've had a discussion recently with my colleagues about what is the best way of writing a loop in C++ that would iterate backward: Count-1, Count-2, ..., 0, using unsigned integer numbers. I'd like to share all possible solutions I managed to gather.
Iterating forward is simple:
unsigned count = 10;
// Forward: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
for(unsigned i = 0; i < count; ++i)
printf("%d ", i);
Iterating backward is equally simple and looks similar, if you use signed integers:
// Backward: 9, 8, 7, 6, 5, 4, 3, 2, 1, 0
// Using signed integer
for(int i = count - 1; i >= 0; --i)
printf("%d ", i);
Same code cannot be used with unsigned integers, because it creates infinite loop, as unsigned number is always >= 0 and just wraps around to maximum value 0xFFFFFFFF:
// WRONG: Inifinte loop, unsigned int wraps around and is always >= 0.
for(unsigned i = count - 1; i >= 0; --i)
printf("%d ", i);
Changing condition to i > 0 is also invalid, because then loop is not executed for i == 0:
// WRONG: Not executed for i == 0.
for(unsigned i = count - 1; i > 0; --i)
printf("%d ", i);
Here comes a bunch of possible valid solutions. My favourite is following for loop:
for(unsigned i = count; i--; )
printf("%d ", i);
Following while loop does same thing. Some people say that it looks more clear. I don't think so, while I believe the for loop is better because it creates local scope for variable i, while the following code does not:
unsigned i = count;
while(i--)
printf("%d ", i);
Another way of implementing exactly same logic is to write the condition like this. It may look like C++ had the "goes to zero" arrow operator -->, but it is actually just (i-- > 0) :)
unsigned i = count;
while(i --> 0)
printf("%d ", i);
Another possible solution of loop condition (a one that does not use the postdecrementation operator) is to compare i with maximum integer value. One disadvantage of it is that you have to carefully match the value of the max constant with type of your iterator - whether it is unsigned int, unsigned short etc.
for(unsigned i = count - 1; i != UINT_MAX; --i)
printf("%d ", i);
Another way of doing this, without using maximum value, is:
for(unsigned i = count - 1; i < count; --i)
printf("%d ", i);
Finally there are solutions possible that introduce second iterator:
// Option 1 using second iterator:
// i goes 0...9, j is inverted i.
for(unsigned i = 0; i < count; ++i)
{
unsigned j = count - i - 1;
printf("%d ", j);
}
// Option 2 using second iterator:
// i goes 10...1, j is decramented i.
for(unsigned i = count; i > 0; --i)
{
unsigned j = i - 1;
printf("%d ", j);
}
Which is your favorite loop? Please leave a comment :)
Comments | #algorithms #c++ Share
# Algorithms for Managing Tree Structure
Sat
04
Feb 2012
What are the ways of storing a tree data structure in memory? I mean a tree with arbitrary number of child nodes. Probably first thing that comes to our minds - as high level programmers - is to dynamically allocate each node as object of some class that would store its data and a collection of pointers to its children. Opposite approach would be to store all nodes in some array - a continuous piece of memory, where each node would refer to other nodes by index or something. Third approach - something in between in terms of sophistication, as well as efficiency - is to have dynamically allocated nodes, but not to store a collection of all child nodes. It is a good idea to employ kind of linked list here. I'd like to describe such data structure and basic algorithms for manipulating it.
The idea is that each node stores - besides its data - 5 pointers (possibly null) to some other nodes: parent, previous sibling, next sibling, first child and last child. It could be seen as equivalent to doubly linked list. It has much more pointers that is needed to be able to traverse whole tree, but thanks to this you can traverse such tree in any order, as well as insert and remove nodes at any point, with best possible time complexity. A node with Parent == null is considered a tree root. Here is a picture of a single node and example tree:
